The Equation of a Line

Computing a Picture

How to draw a line that is not horizontal is obviously the next question. To accomplish that, we need to apply some simple mathematics. One of the math lessons says that a line can be described by one linear function:

f(x) = ax + b

It is common to use horizontal axis of a graph for values of variable x, and to use vertical axis for values of function f(x). But, since coordinates in computer graphics are commonly labeled by names x and y, we can rewrite the equation above as:

y = ax + b

In this equation, x and y are coordinates, or more precisely, the mathematical variable x represents the number of a column, and mathematical variable y represents the number of a row. The mathematical variable b represents the y-intercept, and the mathematical variable a represents the slope of the line.

We need to pick some values for a and b to draw a particular line. Let us choose the value of 0.3 for the slope a and the value 0 for the y-intercept b. The equation is then:

y = 0.3x + 0

Let us draw a piece of the line that is determined by the equation above. Our piece will be a part of the line lying between columns numbered 50 and 500:

    for (int x=50; x<500; x++) {
        int y = 0.3*x + 0;
        putpixel(surface, x, y, makecol(0,0,255) );
        }

The complete program is given below:

#include <allegro.h>

int main()
{
    if (allegro_init()!=0) return 1;
    set_color_depth(32);
    if (set_gfx_mode(GFX_AUTODETECT_WINDOWED, 800, 600, 0, 0)!=0) 
        return 2;
    BITMAP* surface = create_bitmap(SCREEN_W, SCREEN_H);
    install_keyboard();
    clear_to_color(surface, makecol(255,255,255) );
    for (int x=50; x<500; x++) {
        int y = 0.3*x;
        putpixel(surface, x, y, makecol(0,0,255) );
        }
    blit(surface, screen, 0,0,0,0,SCREEN_W,SCREEN_H);
    while (!keypressed())
        rest(20);
    return 0;
}
END_OF_MAIN()

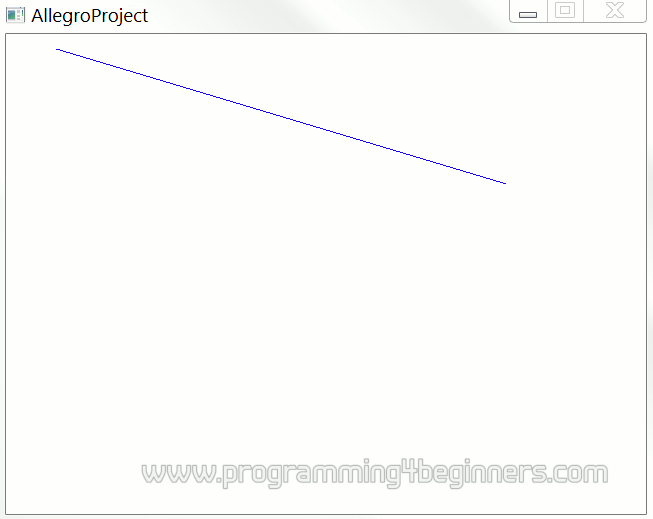
The program produces the image on the right.

However, since the y-intercept b equals 0, should not the line be directed towards the origin in the lower left corner of the image? Also, the slope a is positive, so it would be expected that the line is rising up instead of falling down. In short, this is not quite a line that would be expected given the equation used.

How to explain this strange discrepancy?